УДК 511.522.2

 

С. М. Вахтеров
МГТУ им. Н.Э.Баумана

г. Москва, Россия

 

КРИПТОСИСТЕМА RSA ПРОТИВ ВТФ

 

Мало какая теоретическая проблема математики представлена в Интернет так обширно и спорно, как Великая теорема Ферма. Попытки разных авторов в этом направлении небезынтересны, т.к. накапливают доказательную базу по решению задач в математике.

Данное доказательство теоремы Ферма интересно тем, что для доказательства впервые используются фундаментальные основы криптографической системы RSA. Данный метод можно применить и для решения других уравнений.

 

Введение

Приводимая здесь атака на Великую теорему Ферма (ВТФ) [1],  с целью доказательства отсутствия решений в уравнении: ++ = 0, где e - простое число больше двух, разделена на две части (по следующим условиям):

1)    НОД(φ(x), φ(y), φ(z), e) = 1,

2)    НОД(φ(x), φ(y), φ(z), e) = e.

(Всего две части доказательства, т.к. НОД(φ(x), φ(y), φ(z), e) может принимать только два значения 1 и e. Данное деление доказательства не имеет отношения к  известному делению ВТФ на Случай 1 и Случай 2, определённым в литературе по проблеме Ферма, [1].)

 

Функция Эйлера φ(n),  где n — натуральное число, равна количеству натуральных чисел, не больших n и взаимно простых с ним, [4].  Например,  φ(9) имеет шесть таких чисел: 1, 2, 4, 5, 7 и 8 взаимно простых 9.

 ≡ 1 (mod q), для всех a взаимно простых с q.

Функция Эйлера играет ключевую роль в криптосистеме RSA.

В данной статье доказывается случай, когда x, y, z, e: НОД(e, φ(x), φ(y), φ(z))=1.

 

Арифметические свойства и возможные противоречия

Основные арифметические ограничения ВТФ для основного уравнения теоремы  ++ (где x, y, z, e - целые числа) обобщены в работе Рибенбойма [1], а новые опубликованы в интернет [2]. В данном доказательстве будут использованы следующие свойства основного уравнения Ферма: x+y ≢ z и +  . Далее будет доказано, что результат любого возведения в одну и ту же степень любых двух чисел, несравнимых между собой по модулю третьего числа, противоречит этим свойствам, когда НОД(e, φ(x), φ(y), φ(z))=1.

Обобщенный критерий существования решений
в сравнениях Ферма [3]

Теорема: “Для любого целого числа q и простого числа e, при НОД(e,φ(q))=1, где φ(q) - функция Эйлера от q, существуют целые числа x, y, z, взаимно простые с q,  такие, что +  +  ≡ 0 (mod q) ”.

Доказательство. По предположению НОД(e,φ(q))=1, а значит существуют такие целые числа d и b, что ed=bφ(q)+1. Пусть  целые числа , , , не кратные q, такие, что ++ ≡ 0 (mod q). Тогда, согласно теоремы Эйлера [4]:   ≡ ,  ≡ ,  ≡  (mod q). Поэтому, +  ≡ 0 (mod q).

Пример для  :  , где: =3*11; =3; =7. И, согласно теоремы: +  (mod 33).

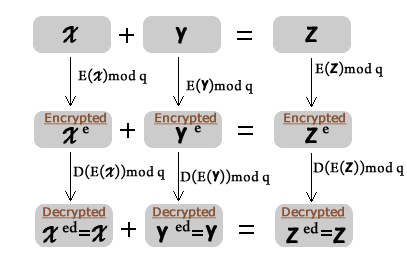
Следствие. Если e ≡ d (mod φ(q)), тогда справедливо сравнение: ++++ ≡ 0 (mod q), а также: +++  +  . Пример: ++, где:  = 5*7; ==5.

 

Создание ключей RSA, для доказательства ВТФ

 

Для поиска обозначенных противоречий, выполним исследование переменных x, y, z основного уравнения ++ в фокусе их возможного использования в качестве ключей криптосистемы RSA[5]. В качестве подобных ключей, для шифрования сообщений, можно рассматривать всевозможные пары чисел, например: (e, x); (e, y); (e, z); (e, ; (e, xy); (e, x+y+1); (e, z +1) и, в общем случае: (e, N) [6].

В доказательстве используются следующие термины RSA:

показатель степени  (encrypted) – используется для шифрования чисел-сообщений.

показатель степени  (decrypted) – используется для расшифрования чисел-криптограмм.

mod x, mod y и, в общем случае:  mod N) – модули (для шифрования и расшифрования сообщений).

Переменные уравнения можно рассматривать в качестве ключей криптосистемы RSA, если значения функций Эйлера чисел, используемых в качестве модулей шифрования (x, y, z или, в общем случае  –  N) не будут кратными числу . (Замечание. Важно отметить, что здесь речь идёт о кратности значений функций Эйлера –  φ(x), φ(y), φ(z), а не кратности самих чисел x, y, z.

Также, для успешной работы криптосистемы RSA, имеются доказанные различными авторами арифметические ограничения:

НОД (x, y, z) =1, [1].

В основу алгоритма RSA заложены свойства простых чисел, а более конкретно – значения функции Эйлера простых чисел. Для правильной работы данной криптосистемы необходимо, чтобы числа-сообщения, были взаимно простыми с модулем ключа шифрования. В нашем случае, это числа x, y, z.

6 < (x or y or z), [2].

 

Шифрование чисел основного уравнения Ферма

 

Допустим условия создания криптосистемы RSA соблюдены и мы имеем ключи для шифрования: (e, x); (e, y); (e, z).

Выполним с их помощью шифрование исходных арифметических ограничений и, сразу же, отметим противоречия с гипотетически возможным решением уравнения.

Сначала рассмотрим результаты шифрования ключа (e, x).

Числа-сообщения – математические вычеты: y (mod x) и -z (mod x). Напомним, что, согласно исходных арифметических ограничений ВТФ:

 y ≢ -z по модулю x, НОД (x, y, z) =1, x > 6.

Криптограммы:  ≡   (mod x) и  ≡   (mod x).

Данные значения степенных вычетов противоречат арифметическим ограничениями ВТФ.

Напомним, что степенной вычет или вычет степени n по модулю N – такое число  , для которого разрешимо сравнение:  ≡  (mod N).

Разные сообщения-вычеты: y и z по модулю x, зашифрованные одним и тем же ключом (e, x), дают разные криптограммы  и . Из этого следует, что:   (mod x). Сравнимость невозможна.

(В общем-то, для криптосистемы было бы абсурдно, если бы два разных сообщения, зашифрованных одним и тем же ключом, давали бы одинаковые криптограммы.)

 

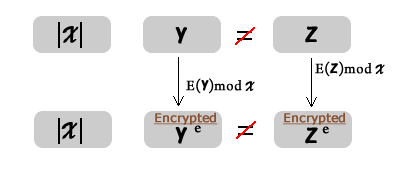
По ключам (e, y) и (e, z) для сообщений (математических вычетов): x  и –z по модулю y, а также для: x и –y по модулю z, также получаются различные криптограммы (вычеты степени e).

Результат атаки на уравнение ВТФ

Таким образом, можно сделать следующий вывод:

“Если хоть одно из чисел x, y, z имеет значение функции Эйлера, которое взаимно просто с e, то теорема Ферма справедлива для всей тройки чисел, т.е. основное уравнение Ферма не имеет решений.”

Этот же вывод можно записать так:

“Если НОД(φ(x), φ(y), φ(z), e) = 1, то основное уравнение Ферма не имеет решений”.

Этот вывод сделан на основании того, что, при указанном условии, возможно создание (из чисел и вычетов тройки чисел ВТФ, а также показателя степени) модели криптосистемы, удовлетворяющей теоретическим основам RSA,

Если  создание ключа для модели криптосистемы RSA возможно, хотя бы по одному числу из тройки  x, y, z, тогда результаты шифрования (степенные вычеты) отличаются и, таким образом, не приводят к гипотетическому решению, т.к. противоречат известным арифметическим ограничениям ВТФ. В свою очередь, предположение, что имеется гипотетическое решение основного уравнения ВТФ, приводит к выводу о неадекватности системы RSA, что тоже невозможно.

Например, если одно из чисел x, y, z является простым числом вида +1, то его функция Эйлера не кратна никаким значениям e [4].

Полученные условия позволяют сосредоточить внимание на доказательстве случая, когда НОД(φ(x), φ(y), φ(z), e) = e, а также продолжить исследования по другим возможным направлениям использования “ключей”, в том числе, для решения не только диафантовых уравнений.

С полученными комментариями по этой статье можно ознакомиться здесь: Комментарии.

 

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

 

1. P. Ribenboim, Fermat's last theorem for amateurs, Springer-Verlag, New York, NY, 1999.

2. Арифметические ограничения для степени p в уравнении Ферма. [Научный форум dxdy - http://dxdy.ru]. – Режим доступа: http://dxdy.ru/topic30942.html (дата обращения 28.03.2010).

3. Вахтеров С.М. Обобщение тривиального случая критерия Вендрта с помощью теоремы Эйлера для любых целых чисел // В мире научных открытий. – 2010. – №3(09). – Часть 1. – С. 119.

4. Euler's_theorem [Vikipedia - http://en.wikipedia.org].  – Режим доступа:  http://en.wikipedia.org/wiki/Euler's_theorem (дата обращения 28.03.2010).

5. RSA [Vikipedia - http://en.wikipedia.org].  – Режим доступа: http://en.wikipedia.org/wiki/RSA (дата обращения 28.03.2010).

6. The RSA Cryptosystem against Last Fermat’s Theorem [2000.ru - http://www.2000.ru].  – Режим доступа:  http:// www.2000.ru (дата обращения 28.03.2010).

 

Contact:

 

http:// www.2000.ru/fermats/2000ru_vsm_RSA_v03ss_01_04_2010.htm

 

Last Modified: May, 12, 2010